Как рассчитывается тепловая нагрузка на систему отопления здания

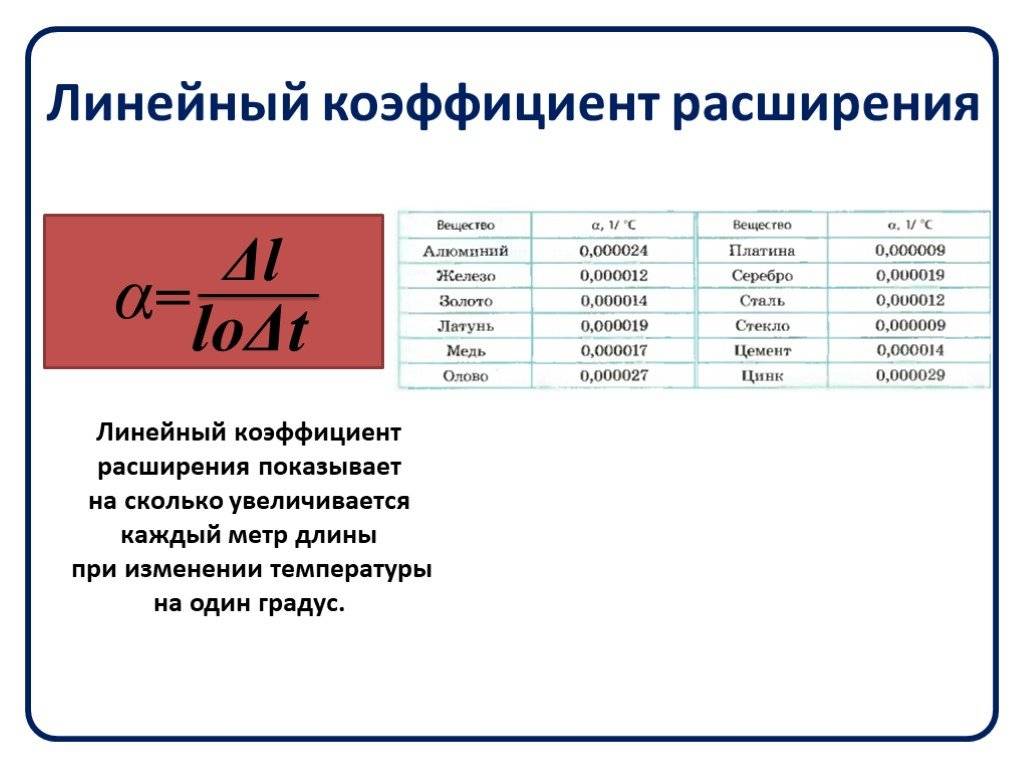
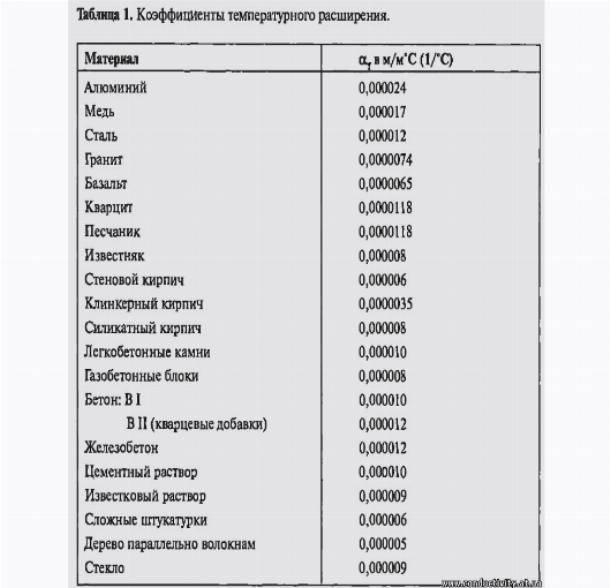
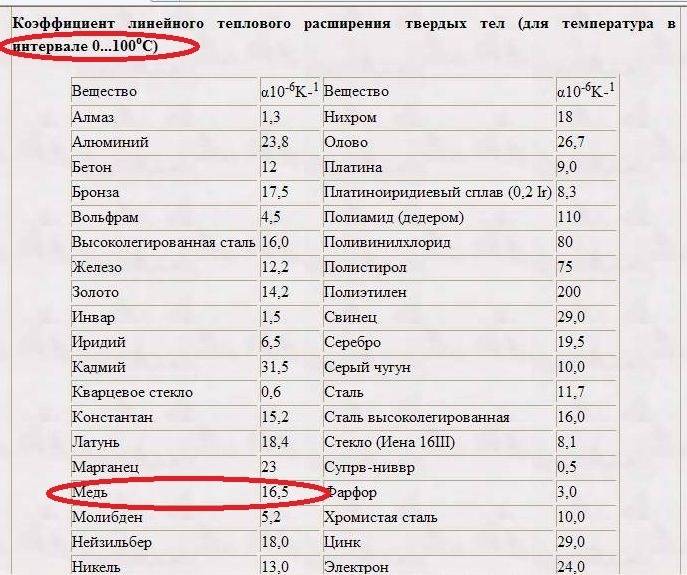
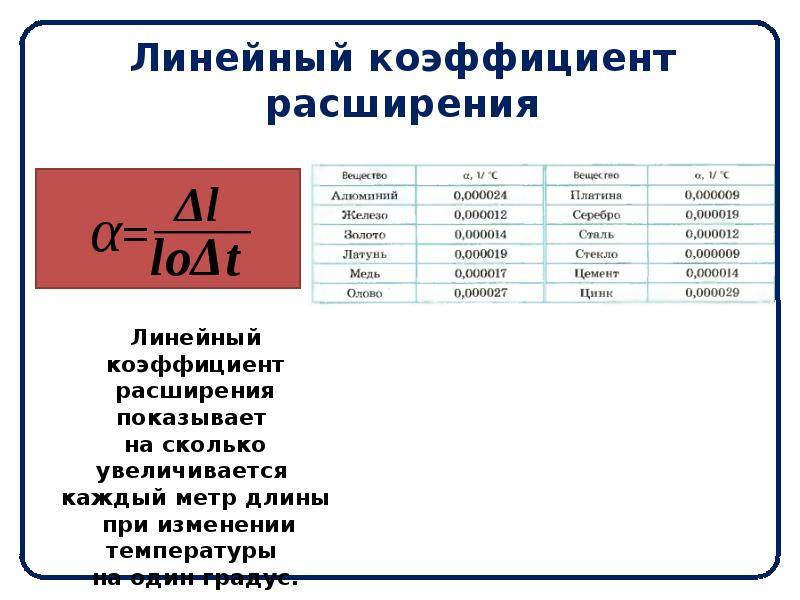
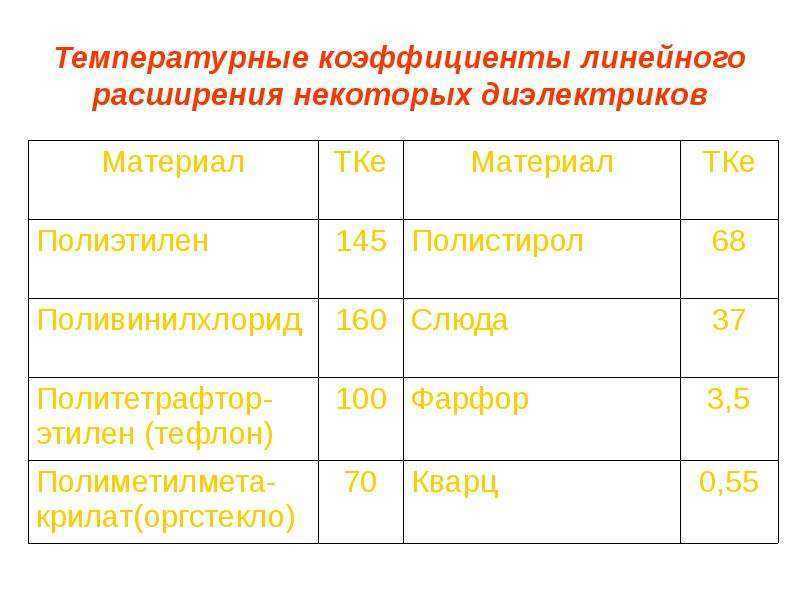
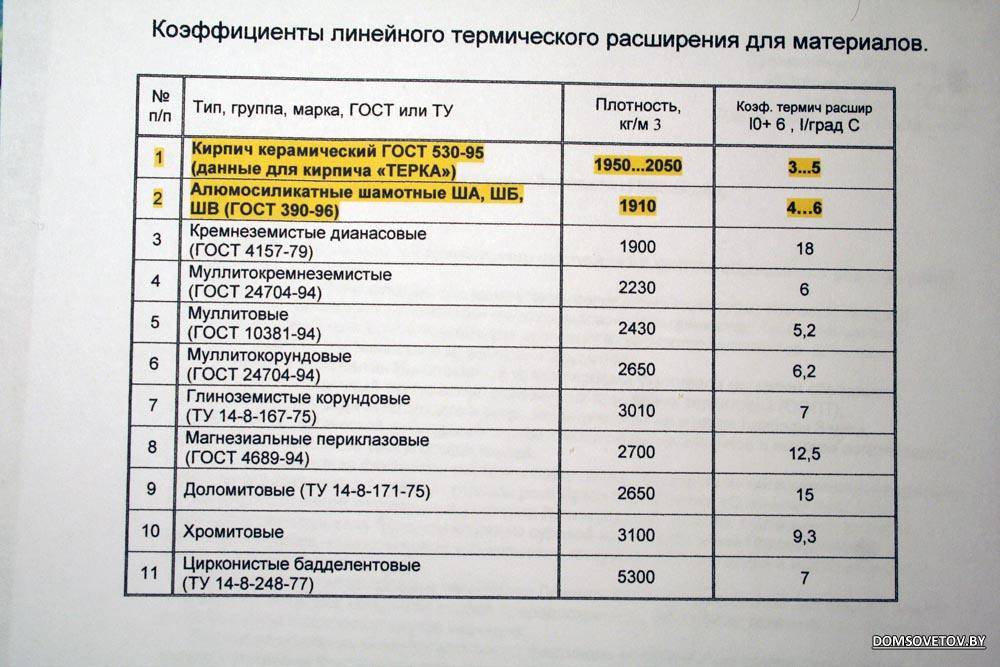
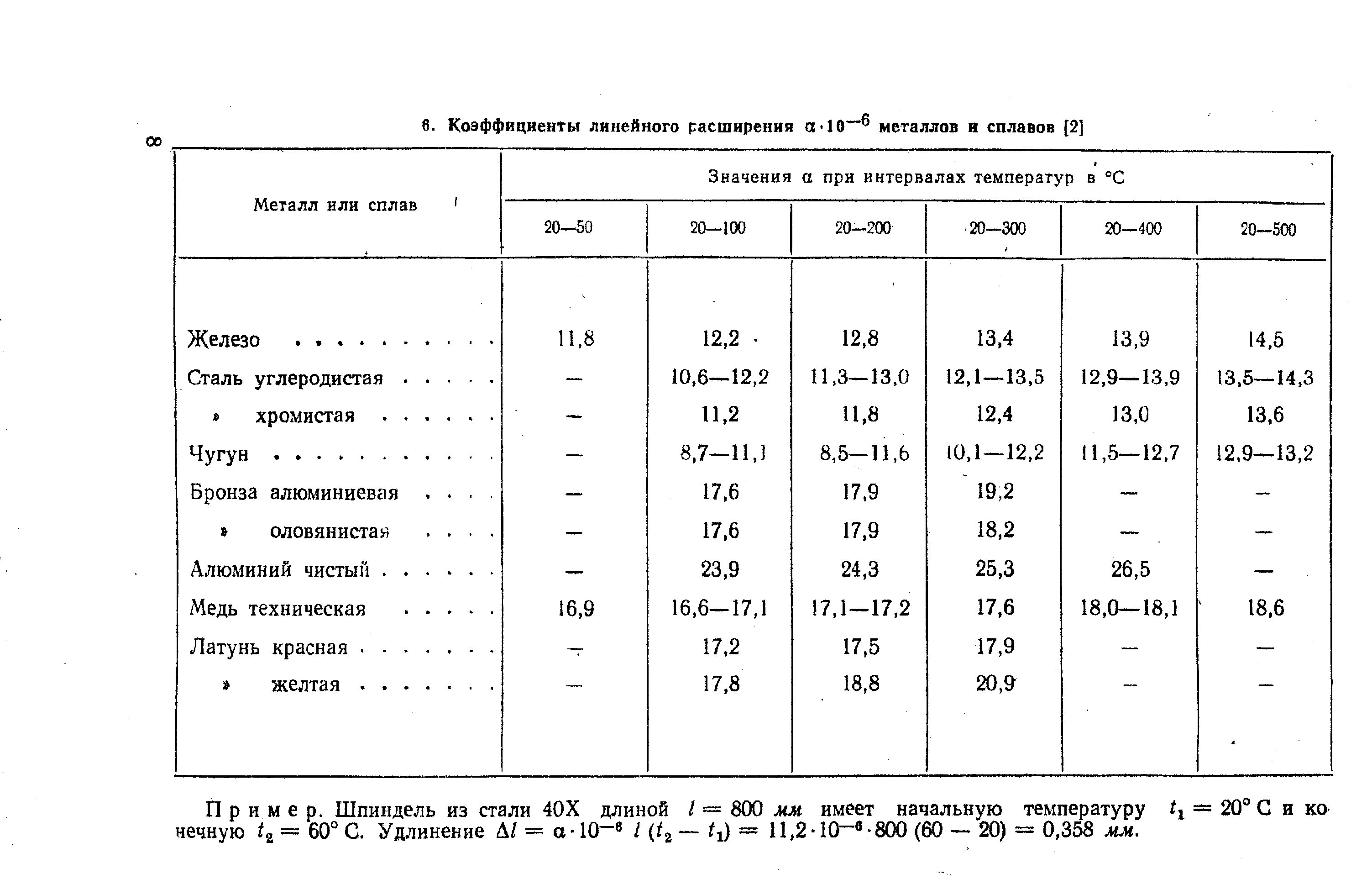
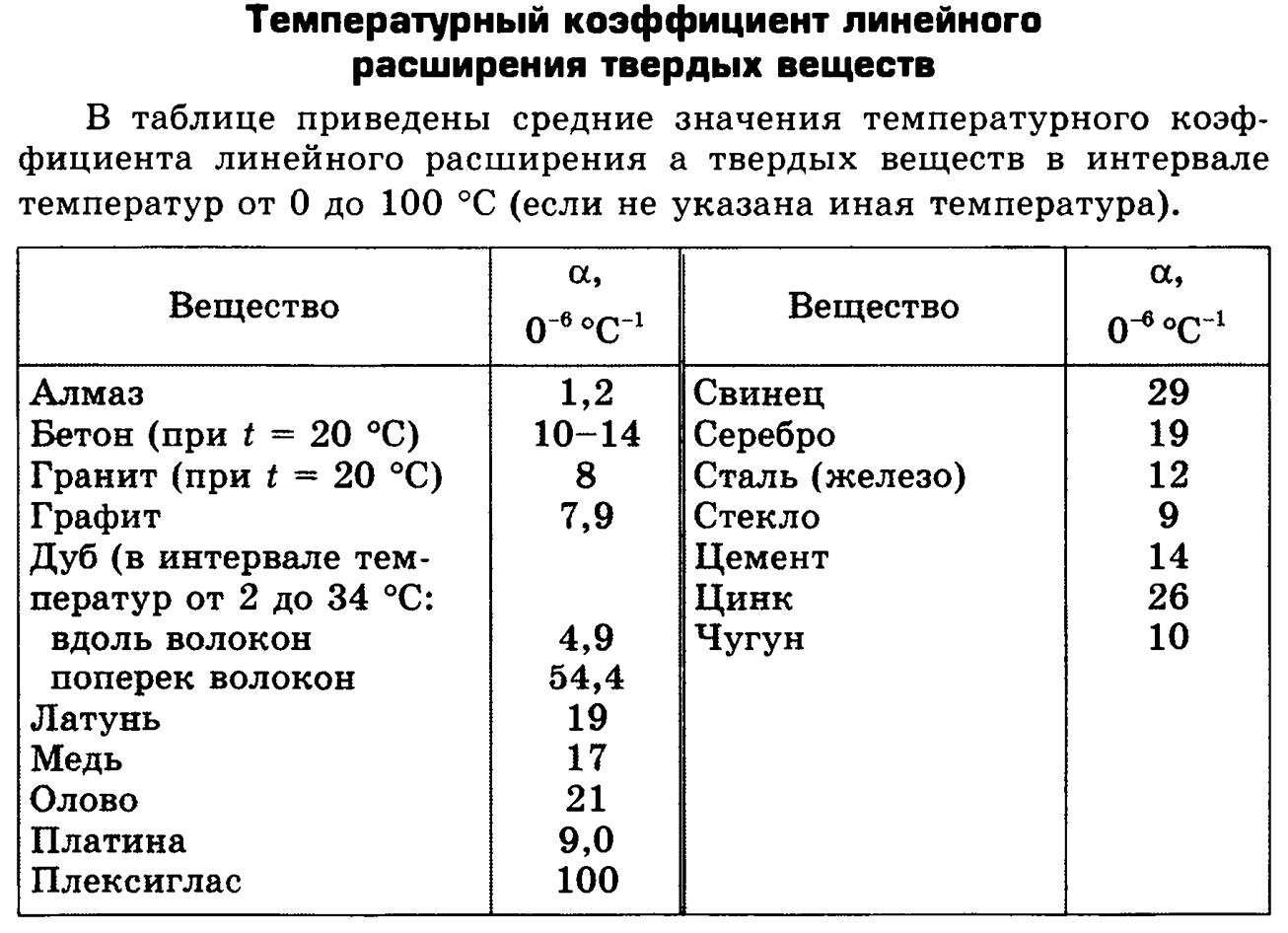
тип

При расчете расширения физического объекта необходимо учитывать, что в зависимости от изменения температуры указанный объект может увеличиваться или уменьшаться в размере..

Некоторые объекты не требуют резкого изменения температуры, чтобы изменить их размер, поэтому вполне вероятно, что значение, полученное в результате расчетов, является средним.

Как и все процессы, тепловое расширение делится на несколько типов, которые объясняют каждое явление в отдельности. В случае твердых веществ типами теплового расширения являются линейное расширение, объемное расширение и поверхностное расширение.

Линейная дилатация

В линейной дилатации преобладает один вариант. В этом случае единственной единицей, которая подвергается изменению, является высота или ширина объекта..

Простой способ рассчитать этот тип расширения – это сравнить значение количества до изменения температуры со значением количества после изменения температуры..

Объемная дилатация

В случае объемного расширения способ его расчета заключается в сравнении объема жидкости до изменения температуры с объемом жидкости после изменения температуры. Формула для расчета:

Поверхностная или площадь дилатации

В случае поверхностного расширения увеличение площади тела или объекта наблюдается при изменении его температуры на 1 ° C..

Это расширение работает для твердых веществ. Если у вас также есть линейный коэффициент, вы можете видеть, что размер объекта будет в два раза больше. Формула для расчета:

_F = A [1 + Я (Т_F – T)]

В этом выражении:

γ = коэффициент расширения площади

= Начальная площадь

_F = Конечная зона

T = Начальная температура.

T_F = Конечная температура

Разница между расширением области и линейным расширением заключается в том, что в первом случае происходит изменение увеличения площади объекта, а во втором – изменение одной единицы измерения (как это может быть длина или ширина физического объекта).

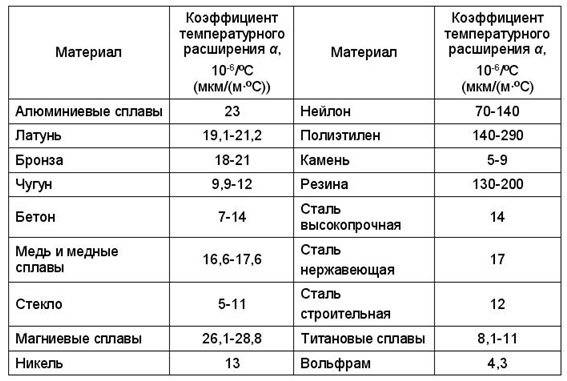
Влияние теплового расширения на разные материалы

Хрупкие материалы

В приведенных выше примерах мы увидели, насколько важно оставлять пространство для расширения при работе с материалами с высоким коэффициентом теплового расширения. В некоторых случаях материалы бывают настолько хрупкими, что разрушаются при резком повышении температуры, даже если могут спокойно двигаться в окружающих их конструкциях

Обычно это происходит, если тело неравномерно нагревается или охлаждается. В этом случае объем также уменьшается или увеличивается неравномерно, и в результате вызванного этим напряжения тело растрескивается или разрушается. Так происходит, например, с изделиями из стекла и керамики.

Для предотвращения термического удара материалы иногда усиливают. При этом внутри них возникают напряжения, обратные деформирующей силе. В некоторых случаях помогают также постепенные нагрев или охлаждение — это позволяет хрупким материалам расширяться постепенно, с минимальным напряжением.

Крышка из закаленного стекла разбивается на мелкие осколки

Коэффициент теплового напряжения материала можно понизить методом комбинирования его с материалом с более низким коэффициентом. Кроме этого коэффициент можно изменить механически, в процессе производства — так делают при изготовлении закалённого стекла. Стекло нередко закаляют после того, как придали ему необходимую форму, иначе оно легко разрушается, если применить к нему силу, например при его резке. Это происходит вследствие возникновения распределенных механических напряжений по объему стеклянного предмета в процессе закалки стекла с помощью нагревания и охлаждения или во время химической обработки.

Для повышения безопасности задние и боковые стекла в автомобилях делают из закаленного стекла. Для еще большей безопасности лобовое стекло состоит из двух слоев закаленного стекла, приклеенных к пленке между ними. Если такое стекло разбить, то осколки остаются на пленке.

Примеры материалов, которые выдерживают высокие температуры и большие перепады температур — закаленные стекло и керамика. Чаще всего их обрабатывают так, чтобы взаимодействие сил по поверхности с силами внутри изделия ограничивало движение молекул с увеличением температуры, и тем самым предотвращало структурную нагрузку, которая обычно присутствует в необработанных стекле и керамике. Обработка бывает механической и химической. Закаленные стекло и керамика растрескиваются при температурах, намного выше температур для необработанных керамики и стекла. Закаленные материалы прочнее обычных, поэтому их нередко используют там, где материалы должны выдерживать большие нагрузки.

Если же закаленное стекло все-таки разбивается, то оно растрескивается на мелкие осколки, а не на большие, как бывает с обычным стеклом. Благодаря этому, закаленное стекло более безопасно и его используют там, где велика вероятность, что это стекло разобьется. Например, чтобы защитить водителя и пассажиров от травм большими осколками стекла в случае аварии, в автомобилях используют именно закаленное стекло.

У некоторых хрупких материалов очень интересные свойства. Хороший пример — изделие из стекла в форме капли, с длинным «хвостом», которое можно сделать, капнув расплавленное стекло в ведро холодной воды. Свойства такого стекла напоминают свойства закаленного стекла. Иногда стекло такой формы называют каплями Принца Руперта

. Во время охлаждения, наружный слой таких капель охлаждается намного быстрее, чем внутренняя часть, поэтому стекло сжато вовнутрь, то есть давление внутри намного больше, чем давление наружного слоя. В результате такая капля хранит большую потенциальную энергию. Благодаря такому распределению сил в капле, более широкая ее часть выдерживает большое напряжение, даже удар молотком. Хвост капли, наоборот, очень хрупок, и если его повредить, то вся капля разлетается на мелкие осколки. Это очень похоже на миниатюрный взрыв. Обычное закаленное стекло нельзя резать после обработки по аналогичным причинам. На сайте YouTube есть множество захватывающих видео взрыва капель Принца Руперта, записанных на высокой скорости 100 000 кадров в секунду и выше.

Поразмышляем

Представьте, что перед вами расположен прямоугольный металлический лист с круглым отверстием посредине. Если металл нагреть, то кусок увеличится из-за теплового расширения. Но что будет с отверстием? Хорошо, давайте возьмем точно такой же лист без отверстия. Нарисуйте на нем круг. Что вы видите? Да, он стал больше. Поэтому и отверстие также увеличится.

С ростом температурного показателя объекты расширяются во всех направлениях. На чертежах видно, что сплошные линии и расширенные границы с пунктирами отмечают исходные границы тел. (а) – Площадь возрастает, потому что растут длина и ширина. (b) – Если убрать заслонку, отверстие увеличится с повышением температуры

Термодинамическое определение

Внутренняя энергия системы является функцией состояния , которая зависит от давления , объема и температуры  :
U{\ displaystyle U}п{\ displaystyle p}V{\ displaystyle V}Т{\ displaystyle T}

Uзнак равнож(п,V,Т){\ Displaystyle U = f (p, V, T)}.

Поскольку эти три переменные связаны уравнением состояния системы, можно, например, выразить бесконечно малое изменение внутренней энергии системы в соответствии с бесконечно малыми изменениями объема и температуры:
U{\ displaystyle U}

dUзнак равно(∂U∂Т)VdТ+(∂U∂V)ТdV{\ displaystyle \ mathrm {d} U = \ left ({\ frac {\ partial U} {\ partial T}} \ right) _ {V} \ mathrm {d} T + \ left ({\ frac {\ partial U} {\ partial V}} \ right) _ {T} \ mathrm {d} V}.

Первый член суммы содержит изменение внутренней энергии как функцию температуры при постоянном объеме, изохорную теплоемкость . Если изменение температуры происходит при постоянном давлении, получаем:
ПРОТИВV{\ Displaystyle \ mathrm {C_ {V}}}

(∂U∂Т)пзнак равноПРОТИВV(Т)+(∂U∂V)Т(∂V∂Т)пзнак равноПРОТИВV(Т)+βV(∂U∂V)Т{\ displaystyle \ left ({\ frac {\ partial U} {\ partial T}} \ right) _ {p} = C_ {V} (T) + \ left ({\ frac {\ partial U} {\ partial V}} \ right) _ {T} \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {p} = C_ {V} (T) + \ beta V \ left ({ \ frac {\ partial U} {\ partial V}} \ right) _ {T}}.

Термин представляет собой изобарный коэффициент теплового расширения системы (коэффициент объемного расширения), он описывает изменение объема при постоянном давлении в зависимости от температуры:
β{\ displaystyle \ beta}

βзнак равно1V(∂V∂Т)пзнак равно-1ρ(∂ρ∂Т)п{\ displaystyle \ beta = {\ frac {1} {V}} \ left ({\ frac {\ partial V} {\ partial T}} \ right) _ {p} = – {\ frac {1} {\ rho}} \ left ({\ frac {\ partial \ rho} {\ partial T}} \ right) _ {p}}.

Обратите внимание, что для идеального газа мы имеем:

βзнак равно1Т{\ displaystyle \ beta = {\ frac {1} {T}}}

В изотропных материалах коэффициент объемного расширения просто связан с коэффициентом линейного расширения  :
β{\ displaystyle \ beta}α{\ displaystyle \ alpha}

βзнак равно3α{\ Displaystyle \ бета = 3 \; \ альфа}

Действительно, бесконечно малое изменение длины куба в трех направлениях пространства приводит к изменению объема
dTHEзнак равноαTHEdТ{\ Displaystyle \ mathrm {d} L = \ alpha \; L \ mathrm {d} T}

βVdТзнак равно3THE2dTHE+3THE(dTHE)2+(dTHE)3{\ Displaystyle \ бета V \; \ mathrm {d} T = 3L ^ {2} \; \ mathrm {d} L + 3 \; L (\ mathrm {d} L) ^ {2} + (\ mathrm { d} L) ^ {3}}

где последние два члена незначительны. Вот как мы получаем .
βзнак равно3α{\ Displaystyle \ бета = 3 \; \ альфа}

На практике коэффициенты теплового расширения и часто выражаются как функция справочного значения для определенной температуры  :
α{\ displaystyle \ alpha}β{\ displaystyle \ beta}Т{\ displaystyle T_ {0}}

βзнак равно1VΔVΔТ{\ displaystyle \ beta = {\ frac {1} {V_ {0}}} {\ frac {\ Delta V} {\ Delta T}}}и .αзнак равно1THEΔTHEΔТ{\ displaystyle \ alpha = {\ frac {1} {L_ {0}}} {\ frac {\ Delta L} {\ Delta T}}}

Эта формула действительна в тех случаях, когда изменение длины линейно зависит от изменения температуры, но не для больших интервалов температур или если материал претерпевает фазовый переход в рассматриваемом интервале. В общем случае температурная зависимость объемного коэффициента теплового расширения выражается соотношением Грюнайзена
β{\ displaystyle \ beta}

βχТПРОТИВVρзнак равноγ≃постоянный{\ displaystyle {\ frac {\ beta} {\ chi _ {T} C_ {V} \ rho}} = \ gamma \ simeq {\ mbox {constant}}}

где это изотермическая сжимаемость материала, его изохорной теплоемкости, ее плотность и от параметра Грюнайзены . Так как и в первом приближении не зависят от температуры, тепловые изменения компенсируют вариации .
χТ{\ displaystyle \ chi _ {T}}ПРОТИВV{\ displaystyle C_ {V}}ρ{\ displaystyle \ rho}γ{\ displaystyle \ gamma}χТ{\ displaystyle \ chi _ {T}}ρ{\ displaystyle \ rho}ПРОТИВV{\ displaystyle C_ {V}}β{\ displaystyle \ beta}

1.5. Температурные перемещения

Вернемся к бруску материала, показанного на рисунке 1 . Предполагаем, что материал бруска является гомогенным и изотропным, то есть механические свойства материала бруска являются одинаковыми во всем его объеме. Кроме того, предполагаем, что изменение температуры ΔT

является однородным, то есть одинаковым, по всему бруску. При таких условиях мы можем вычислить увеличение любого размера бруска путем умножения первоначального размера на температурную деформацию. Например, если один из размеров бруска составляет L, то этот размер увеличиться на величину

δТ = εT·L=α·ΔT·L (4) Уравнение (4) можно применять для вычисления изменений длин элементов конструкций после однородного нагрева, например, удлинение призматического стержня на рисунке 2.2. Поперечные размеры стержня также изменятся, но эти изменения не показаны на рисунке 2.2, так как обычно они не оказывают влияния на осевые силы, которые передаются этим стержнем.

Рисунок 2.2 – Увеличение длины призматического стрежня в результате однородного увеличения температуры (уравнение (4))

Пример.

Оценим удлинение незакрепленных алюминиевого и стального стержней длиной 3 м при увеличении их температуры на 50 ºС.

Для алюминиевого стержня:

δТ =α·ΔT·L = 23·10-6·50·3000 = 3,5 мм Для стержня из малоуглеродистой стали:

δТ =α·ΔT·L = 12·10-6·50·3000 = 1,8 мм При рассмотрении выше температурных деформаций предполагалось, что конструкция не имеет ограничений для своих перемещений, что позволяло ей расширяться или сокращаться совершенно свободно. Такие условия возникают, например, когда объект лежит на гладкой поверхности, на которой не возникает трения . В таких случаях при однородном нагреве всего объекта в целом не возникает напряжений, хотя неоднородные изменения температуры могут вызывать внутренние температурные напряжения. Однако многие конструкции имеют опоры, которые препятствуют свободному расширению и сокращению их размеров. Поэтому в них развиваются температурные напряжения даже, если изменение температуры является однородным по всей конструкции.

Пример перерасчета и уменьшения тепловых нагрузок

Далее мы рассмотрим пример реального уменьшения тепловых нагрузок и затрат на отопления на одном из выполненных нами объектов.

Объект №1 – помещение коммерческого назначения

Помещение коммерческого назначения на первом этаже пяти-этажного здания в Москве.

Основные данные по объекту:

Адрес объекта	г. Москва
Этажность здания	5 этажей
Этаж на котором расположены обследуемые помещения	1-й
Площадь обследуемых помещений	112,9 м2
Высота этажа	3,0 м
Система отопления	Однотрубная
Температурный график	95-70 оС
Расчетный температурный график для этажа на котором находится помещение	75-70 оС
Тип розлива	Верхний
Расчетная температура внутреннего воздуха	+ 20 оС
Отопительные радиаторы, тип, количество	Радиаторы чугунные М-140-АО – 6 шт. Радиатор биметаллический Global (Глобал) – 1 шт.
Диаметр труб системы отопления, мм	Ду25
Длина подающего трубопровода системы отопления, м	L = 28,0 м.

Горячее водоснабжение и вентиляция на данном объекте отсутствовали.

Договорные тепловые нагрузки составляли 0,02 Гкал/час или 47,67 Гкал/год.

Расчет теплопередачи установленных радиаторов отопления с учетом потерь в трубопроводах и способа установки составил 0,007454 Гкал/час.

Максимальный часовой расход на отопление в трубопроводах составил 0.001501 Гкал/час.

В итоге, максимальный часовой расход на отопление составил 0,008955 Гкал/час или 23 Гкал/год.

Годовая экономия = 47,67 – 23 = 24,67 Гкал/год.

При средней стоимости Гкал 1,7 тысяч рублей, годовая экономия на отоплении для объекта площадью 112 м. кв. составила 42 тысячи рублей.

Отрицательное тепловое расширение

Отрицательное тепловое расширение происходит в некоторых материалах, которые вместо увеличения размера при высоких температурах сжимаются из-за низких температур.

Этот тип теплового расширения обычно наблюдается в открытых системах, где наблюдаются направленные взаимодействия, как в случае со льдом, или в сложных соединениях, как это происходит с некоторыми цеолитами, в том числе с Cu2O.

Аналогичным образом, некоторые исследования показали, что отрицательное тепловое расширение также происходит в однокомпонентных решетках в компактной форме и с центральным силовым взаимодействием.

Наглядный пример отрицательного теплового расширения можно увидеть, когда мы добавляем лед в стакан с водой. В этом случае высокая температура жидкости на льду не вызывает какого-либо увеличения размера, а, скорее, размер льда уменьшается.

Формулы расчёта

Исходя из общих потребностей здания в тепловой энергии и технических характеристик постройки, с целью определения оптимального количества теплоты за единицу времени могут использоваться разные стандартные формулы.

При отсутствии приборов учёта: Q = V × (Тх - Тy) / 1000

Обозначение	Параметр
V	Объём теплового носителя в отопительной системе
Тх	Показатели температурного режима нагретого теплоносителя (60-65оС)
Тy	Исходная температура не нагретого теплового носителя
1000	Стандартный поправочный числовой множитель

Схема отопления с замкнутым типом контура:

Qот = α × qо × V × (Тв - Тн.р) × (1 + Kн.р) × 0,000001

Обозначение	Параметр
α	Корректирующий погодные характеристики числовой множитель при уличном температурном режиме, отличном от минус 30оС
V	Показатели объёма строения в соответствии с наружными замерами
qо	Отопительный удельный показатель при температурном режиме -30оС
tв	Расчётные показатели внутреннего температурного режима в строении
tн.р	Расчётный режим наружного температурного режима для проектирования отопительной системы
Kн.р	Поправочный числовой множитель в виде соотношения теплопотерь с инфильтрацией и тепловой передачей посредством внешних конструктивных элементов

Применение поправочного числового множителя

При выполнении расчётов тепловой нагрузки обязательно учитывается поправочный числовой множитель, при помощи которого определяется отличие расчётного температурного режима наружного воздуха для проектов отопительных систем. В таблице представлены поправочные числовые множители для различных климатических зон, расположенных на территории Российской Федерации.

-35оС	-36оС	-37оС	-38оС	-39оС	-40оС
0,95	0,94	0,93	0,92	0,91	0,90

В других регионах России, где расчётный температурный режим наружных воздушных масс при проектировании отопительной системы находится на уровне минус 31°С или ниже, значения расчётных температур внутри обогреваемых помещений принимаются в соответствии с данными, приведёнными в действующей редакции СНиП 2.08.01-85.

На что обратить внимание при расчётах

В соответствии с действующим СНиП, на каждые 10 м2 обогреваемой площади должно приходится не менее 1 кВт тепловой мощности, но при этом в обязательном порядке учитывается так называемый региональный поправочный числовой множитель:

• зона с умеренными климатическими условиями – 1.2-1.3;
• территория южных регионов – 0.7-0.9;
• районы крайнего севера – 1.5-2.0.

Кроме прочего, немаловажное значение имеет высота потолочных конструкций и индивидуальные тепловые потери, которые напрямую зависят от типовых характеристик эксплуатируемого строения. Как правило, на каждый кубометр полезной площади затрачивается 40 ватт тепловой энергии, но при выполнении расчётов потребуется также учитывать следующие поправки:

• наличие окна – плюс 100 ватт;
• наличие двери – плюс 200 ватт;
• угловое помещение – поправочный числовой множитель 1.2-1.3;
• торцевая часть здания – поправочный числовой множитель 1.2-1.3;
• частное домовладение – поправочный числовой множитель 1.5.

Практическое значение имеют показатели потолочного и стенового сопротивления, потери тепла через конструкции ограждающего типа и функционирующую вентиляционную систему.

Вид материала	Уровень термического сопротивления
Кирпичная кладка в три кирпича	0,592 м2 × с/Вт
Кирпичная кладка в два с половиной кирпича	0,502 м2 × с/Вт
Кирпичная кладка в два кирпича	0,405 м2 × с/Вт
Кирпичная кладка в один кирпич	0,187 м2 × с/Вт
Газосиликатные блоки толщиной 200 мм	0,476 м2 × с/Вт
Газосиликатные блоки толщиной 300 мм	0,709 м2 × с/Вт
Бревенчатые стены толщиной 250 мм	0,550 м2 × с/Вт
Бревенчатые стены толщиной 200 мм	0,440 м2 × с/Вт
Бревенчатые стены толщиной 100 мм	0,353 м2 × с/Вт
Деревянный неутеплённый пол	1,85 м2 × с/Вт
Двойная деревянная дверь	0,21 м2 × с/Вт
Штукатурка толщиной 30 мм	0,035 м2 × с/Вт
Каркасные стены толщиной 20 см с утеплением	0,703 м2 × с/Вт

В результате функционирования вентиляционной системы потери тепловой энергии в зданиях составляют порядка 30-40%, через кровельные перекрытия уходит примерно 10-25%, а сквозь стены – около 20-30%, что должно учитываться при проектировании и расчёте тепловой нагрузки.

Виды тепловых нагрузок

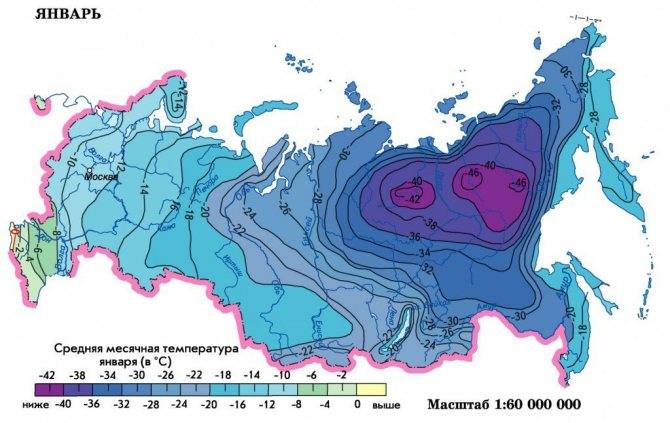
При расчетах учитывают средние сезонные температуры Тепловые нагрузки носят разный характер. Есть некоторый постоянный уровень теплопотерь, связанный с толщиной стены, конструкцией кровли. Есть временные – при резком снижении температуры, при интенсивной работе вентиляции. Расчет всей тепловой нагрузки учитывает и это.

Сезонные нагрузки

Так называют теплопотери, связанные с погодой. Сюда относят:

• разницу между температурой наружного воздуха и внутри помещения;
• скорость и направление ветра;
• количество солнечного излучения – при высокой инсоляции здания и большом количестве солнечных дней даже зимой дом охлаждается меньше;
• влажность воздуха.

Сезонную нагрузку отличает переменный годовой график и постоянный суточный. Сезонная тепловая нагрузка – это отопление, вентиляция и кондиционирование. К зимним относят 2 первых вида.

Постоянные тепловые

Промышленное холодильное оборудование выделяет большое количество тепла К круглогодичным относят горячее водоснабжение и технологические аппараты. Последние имеет значение для промышленных предприятий: варочные котлы, промышленные холодильники, пропарочные камеры выделяют гигантское количество тепла.

В жилых зданиях нагрузка на горячее водоснабжение становится сравнима с отопительной нагрузкой. Величина эта мало изменяется в течение года, но сильно колеблется в зависимости от времени суток и дня недели. Летом расход ГСВ уменьшается на 30%, так как температура воды в холодном водопроводе выше на 12 градусов, чем зимой. В холодное время года потребление горячей воды растет, особенно в выходные дни.

Сухое тепло

Комфортный режим определяется температурой воздуха и влажностью. Эти параметры рассчитывают, руководствуясь понятиями сухого и скрытого тепла. Сухое – это величина, измеряемая специальным сухим термометром. На нее воздействует:

• остекление и дверные проемы;
• солнце и тепловые нагрузки на зимнее отопление;
• перегородки между комнатами с разной температурой, полы над пустым пространством, потолки под чердаками;
• трещины, щели, зазоры в стенах и дверях;
• воздуховоды вне отапливаемых зон и вентиляция;
• оборудование;
• люди.

Полы на бетонном фундаменте, подземные стены при расчетах не учитываются.

Скрытое тепло

Влажность помещения повышает температуру внутри Этот параметр определяет влажность воздуха. Источником выступает:

• оборудование – нагревает воздух, снижает влажность;
• люди – источник влажности;
• потоки воздуха, проводящие сквозь трещины и щели в стенах.

Точные расчеты тепловой нагрузки

Значение теплопроводности и сопротивление теплопередачи для строительных материалов

Но все же этот расчет оптимальной тепловой нагрузки на отопление не дает требуемую точность вычисления. Он не учитывает важнейший параметр – характеристики здания. Главной из них является сопротивление теплопередачи материал изготовления отдельных элементов дома – стен, окон, потолка и пола. Именно они определяют степень сохранения тепловой энергии, полученной от теплоносителя системы отопления.

Что же такое сопротивление теплопередачи (R)? Это величина, обратная теплопроводности (λ) – возможности структуры материала передавать тепловую энергию. Т.е. чем больше значение теплопроводности – тем выше тепловые потери. Для расчета годовой нагрузки на отопление воспользоваться этой величиной нельзя, так как она не учитывает толщину материала (d). Поэтому специалисты используют параметр сопротивление теплопередачи, который вычисляется по следующей формуле:

R=d/λ

Расчет по стенам и окнам

Сопротивление теплопередачи стен жилых зданий

Существуют нормированные значения сопротивления теплопередачи стен, которые напрямую зависят от региона, где расположен дом.

В отличие от укрупненного расчета нагрузки на отопление сначала нужно вычислить сопротивление теплопередачи для наружных стен, окон, пола первого этажа и чердака. Возьмем за основу следующие характеристики дома:

• Площадь стен – 280 м². В нее включены окна – 40 м²;
• Материал изготовления стен – полнотелый кирпич (λ=0.56). Толщина наружных стен – 0,36 м. Исходя из этого рассчитываем сопротивление телепередачи — R=0.36/0.56= 0,64 м²*С/Вт;
• Для улучшения теплоизоляционных свойств был установлен наружный утеплитель – пенополистирол толщиной 100 мм. Для него λ=0,036. Соответственно R=0,1/0,036= 2,72 м²*С/Вт;
• Общее значение R для наружных стен равно 0,64+2,72= 3,36 что является очень хорошим показателем теплоизоляции дома;
• Сопротивление теплопередачи окон — 0,75 м²*С/Вт (двойной стеклопакет с заполнением аргоном).

Фактически тепловые потери через стены составят:

(1/3,36)*240+(1/0.75)*40= 124 Вт при разнице температуры в 1°С

Температурные показатели возьмем такие же, как и для укрупненного вычисления нагрузки на отопление +22°С в помещении и -15°С на улице. Дальнейший расчет необходимо делать по следующей формуле:

124*(22+15)= 4,96 кВт/час

Расчет по вентиляции

Затем необходимо вычислить потери через вентиляцию. Общий объем воздуха в здании составляет 480 м³. При этом его плотность примерно равна 1,24 кг/м³. Т.е. его масса равна 595 кг. В среднем за сутки (24 часа) происходит пятикратное обновление воздуха. В таком случае для вычисления максимальной часовой нагрузки для отопления нужно рассчитать тепловые потери на вентиляцию:

(480*40*5)/24= 4000 кДж или 1,11 кВт/час

Суммируя все полученные показатели можно найти общие тепловые потери дом:

4,96+1,11=6,07 кВт/час

Таким образом определяется точная максимальная тепловая нагрузка на отопление. Полученная величина напрямую зависит от температуры на улице. Поэтому для расчета годовой нагрузки на отопительную систему нужно учитывать изменение погодных условий. Если средняя температура в течение отопительного сезона составляет -7°С, то итоговая нагрузка на отопление будет равна:

(124*(22+7)+((480*(22+7)*5)/24))/3600)*24*150(дней отопительного сезона)=15843 кВт

Меняя температурные значения можно сделать точный расчет тепловой нагрузки для любой системы отопления.

Полученная величина указывает на фактические затраты энергоносителя при работе системы. Существует несколько способов регулирования тепловой нагрузки отопления. Наиболее действенный из них – уменьшение температуры в комнатах, где нет постоянного присутствия жильцов. Это можно осуществить с помощью терморегуляторов и установленных датчиков температуры. Но при этом в здании должна быть установлена двухтрубная система отопления.

Для вычисления точного значения тепловых потерь можно воспользоваться специализированной программой Valtec. В видеоматериале показа пример работы с ней.